Распознаватель адресов. Пусть ставится задача создания автомата, распознающего допустимые адреса электронной почты, которые представлены регулярным выражением:
[a-zA-Z0-9._-]+@[a-zA-Z0-9._-]+\.[a-zA-Z]
Входная лента содержит строки: enin@moskou и enin@moskou.ru, которые проверяются на корректность.
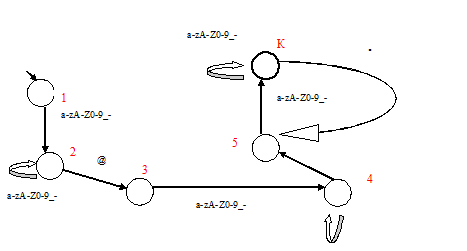
На рисунке представлен конечный автомат, принимающий входные цепочки и принимающий решение о том, принадлежит ли входная цепочка множеству допустимых адресов электронной почты.
Начальное состояние – 1, конечное (допустимое) - К. Говорят, что автомат допускает цепочку (строку), если эта цепочка переводит его в одно из допустимых состояний. В противном случае – автомат отвергает строку. Множество всех строк, допускаемых автоматом, образуют язык, им распознаваемый.
Элементы регулярных выражений, использованные для описания строк языка адресов электронной почты, приведены в приложении к тексту лекции: таблица А. Элементы регулярных выражений в Microsoft.NET
Компиляция - лексический анализ. Этап лексического анализа при компиляции заключается в том, что текст исходной программы разбивается на последовательность лексем.
Теперь мы рассмотрим этот процесс не с позиции его описания средствами НФБ - грамматики, а опишем машинную модель распознавателя лексем.
- Любой идентификатор должен начинаться с буквы; пока символы, следующие за ней, являются цифрами или буквами, они входят в имя этого идентификатора;
- Целое число – просто последовательность цифр;
- Зарезервированное слово if – это последовательность из двух символов;
Во всех этих случаев для распознавания лексем применяется простая модель под названием КОНЕЧНЫЙ АВТОМАТ (КА) или машина состояний. Пока мы знаем, в каком из состояний находимся, мы можем определить, является ли очередной вводимый символ частью лексемы, которую мы ищем.
Рассмотрим простой КА, задача которого – распознавать двоичные цепочки с нечетным количеством единиц (рис. 5.1). Процесс начинается с состояния А (содержащего дугу ввода, не выходящую из другого состояния), затем в зависимости от следующего введенного символа автомат переходит в одно из состояний, А или В, двигаясь вдоль дуги, помеченной этим символом. Очевидно, что состояние В (конечное состояние, обозначенное двойным кружком) соответствует нечетному количеству единиц во введенной цепочке. Поэтому, пока автомат находится в состоянии В, введенная на данный момент цепочка удовлетворяет предъявленному требованию и допускается автоматом. Когда автомат находится в состоянии А, такая цепочка не допускается.
Пусть на входе имеем цепочку 100101. Рассмотрим последовательность действий КА.
| Ввод |
Текущее состояние |
Допускается ли цепочка |
| Null |
А |
Нет |
| 1 |
В |
Да |
| 10 |
В |
Да |
| 100 |
В |
Да |
| 1001 |
А |
Нет |
| 10010 |
А |
Нет |
| 100101 |
В |
Да |
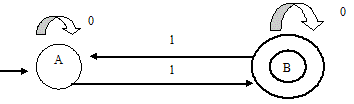
Рис. 5.1. КА, распознающий битовые цепочки с нечетным количеством единиц.
На рис. 5.2 изображен другой КА, распознающий целые числа со знаком. В расширенной нотации мы определили такие числа как: <целое со знаком>::=[+|-]<целое> {<целое>}*. Этот пример иллюстрирует еще одно важное свойство КА: между абстрактными машинами и грамматиками существует взаимное соответствие или КА может быть смоделирован при помощи грамматики.
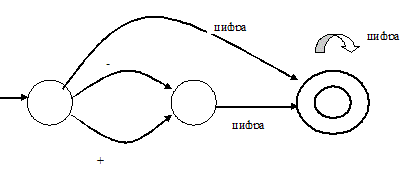
Рис. 5.2. КА, распознающий целые числа с необязательным знаком
Похожие статьи: